1. Introduction machine learning
  2. Mathematics for Machine Learning

Mathematics for Machine Learning

Machine learning may seem like magic, but behind that magic is mathematics. To truly understand how algorithms work, you need to be familiar with key mathematical concepts. This chapter will cover the essentials of Linear Algebra, Probability and Statistics, and Calculus. These form the bedrock of machine learning, helping you build better models, optimize algorithms, and interpret results effectively.

2.1 Linear Algebra Essentials

Linear algebra deals with vectors, matrices, and operations involving them. Machine learning algorithms often rely on linear algebra to represent and manipulate data efficiently.

Key Concepts in Linear Algebra

  1. Vectors
    A vector is an array of numbers arranged in a single row (row vector) or column (column vector). Vectors represent points in space, such as features in a dataset. Example:
    A 3-dimensional vector: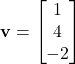 \mathbf{v} = \begin{bmatrix} 1 \\ 4 \\ -2 \end{bmatrix}
  2. Matrices
    A matrix is a two-dimensional array of numbers. In machine learning, matrices are used to represent datasets, where each row is a data point and each column is a feature. Example:
    A 3×2 matrix: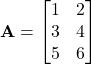 \mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}
  3. Matrix Operations
    • Addition: Matrices of the same size can be added element-wise.
    • Scalar Multiplication: Multiply every element in a matrix by a constant.
    • Matrix Multiplication: Combining two matrices to produce a new matrix.
    Example of Matrix Multiplication: \mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 5 \\ 6 \end{bmatrix} \mathbf{A} \times \mathbf{B} = \begin{bmatrix} (1 \times 5) + (2 \times 6) \\ (3 \times 5) + (4 \times 6) \end{bmatrix} = \begin{bmatrix} 17 \\ 39 \end{bmatrix}
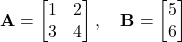
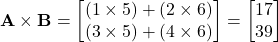
  4. Transpose of a Matrix
    Flipping a matrix along its diagonal. Rows become columns and vice-versa. Example: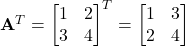 \mathbf{A}^T = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^T = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}
  5. Dot Product
    The dot product of two vectors measures how similar they are. Example: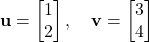 \mathbf{u} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}, \quad \mathbf{v} = \begin{bmatrix} 3 \\ 4 \end{bmatrix} \mathbf{u} \cdot \mathbf{v} = (1 \times 3) + (2 \times 4) = 3 + 8 = 11

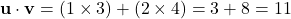
Why Linear Algebra Matters in ML

  • Data Representation: Datasets are often stored as matrices, and individual features are represented as vectors.
  • Transformations: Algorithms like PCA (Principal Component Analysis) use linear algebra to reduce dimensions.
  • Neural Networks: Operations in neural networks rely heavily on matrix multiplication.

2.2 Probability and Statistics Overview

Probability and statistics help machine learning models understand uncertainty and variation in data. Understanding these concepts allows you to build models that can make predictions reliably.

Key Concepts in Probability

  1. Probability Basics
    Probability measures the likelihood of an event occurring. Formula: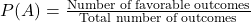 P(A) = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}} Example: Rolling a 6-sided die and getting a 4: P(\text{Rolling a 4}) = \frac{1}{6}
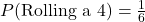
  2. Conditional Probability
    The probability of event A happening given that event B has already happened. Formula: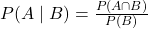 P(A \mid B) = \frac{P(A \cap B)}{P(B)}
  3. Bayes’ Theorem
    Helps in updating the probability of an event based on new evidence. Formula: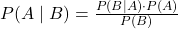 P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}
  4. Probability Distribution
    • Normal Distribution: Bell-shaped curve; many natural phenomena follow this distribution.
    • Bernoulli Distribution: Binary outcomes (e.g., coin flips).
    • Poisson Distribution: Counts of events over time (e.g., number of calls to a customer service line).

Key Concepts in Statistics

  1. Descriptive Statistics
    • Mean: Average value.
    • Median: Middle value in a sorted list.
    • Mode: Most frequent value.
    • Standard Deviation: Measure of data spread.
  2. Inferential Statistics
    • Hypothesis Testing: Testing assumptions about data (e.g., A/B testing).
    • Confidence Intervals: Range where a population parameter likely falls.

Why Probability and Statistics Matter in ML

  • Model Evaluation: Metrics like accuracy, precision, and recall rely on probability.
  • Uncertainty Management: Probabilistic models like Naive Bayes use these concepts.
  • Data Insights: Statistical analysis helps in understanding patterns in data.

2.3 Calculus Basics for ML

Calculus helps optimize machine learning models by understanding how changes in input affect the output. In ML, calculus is primarily used for gradient-based optimization.

Key Concepts in Calculus

  1. Derivatives
    A derivative measures the rate of change of a function. Example: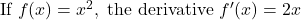 \text{If } f(x) = x^2, \text{ the derivative } f'(x) = 2x
  2. Gradient
    The gradient is the vector of partial derivatives, showing the direction of steepest ascent. Example: \text{For } f(x, y) = x^2 + y^2: \quad \nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right] = [2x, 2y]
  3. Chain Rule
    Used when a function is composed of other functions. Example: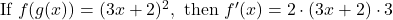 \text{If } f(g(x)) = (3x + 2)^2, \text{ then } f'(x) = 2 \cdot (3x + 2) \cdot 3
  4. Optimization with Gradients
    Gradient Descent is an optimization technique to minimize the loss function in ML models. The idea is to update model parameters by taking steps in the direction of the negative gradient. Update Rule: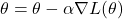 \theta = \theta - \alpha \nabla L(\theta) Where:
    • θ\theta: Model parameter
    • α\alpha: Learning rate
    • ∇L(θ)\nabla L(\theta): Gradient of the loss function

Why Calculus Matters in ML

  • Training Models: Neural networks use calculus for backpropagation.
  • Optimization: Minimizing loss functions to improve model accuracy.
  • Learning Rates: Fine-tuning learning rates for better convergence.

Conclusion

In this chapter, we’ve covered the essential mathematical tools needed for machine learning: Linear Algebra, Probability and Statistics, and Calculus. Mastering these concepts will give you a deeper understanding of how algorithms work under the hood and help you develop more robust models.

Scroll to Top