Linear Regression

Linear Regression is one of the most fundamental and widely used algorithms in Machine Learning. Even though it sounds technical, the idea behind it is very simple — we try to understand and predict how one value (for example, the price of a house) changes with respect to another value (for example, its size or number of rooms).

What is Regression?

Regression is a type of supervised machine learning technique used to predict a continuous numerical value based on past data. It analyzes the relationship between input variables (also called features) and output variables (target value) to make predictions.

To understand it easily:

If we want to predict a number, like temperature, price, marks, salary, etc., we use Regression.
If we want to classify something into categories, like spam or not spam, male or female, dog or cat, we use Classification.

So, Regression = prediction of numbers.
Classification = prediction of labels or categories.

Example for better understanding:

Imagine you run a small shop and want to predict your daily sales based on temperature. From your past data, you notice when the temperature increases, more people buy cold drinks and your sales increase. So, you try to predict the sales for tomorrow based on the temperature forecast. This is an example of regression.

Why Linear Regression Matters in Machine Learning?

Linear Regression is important because:

It is simple and easy to understand — It follows basic mathematics and gives predictions using a straight-line relationship.
Works well with real-world numerical data — Many situations in business, science, and economics follow linear patterns.
Helps in understanding relationships between variables — It not only predicts values but also tells how strongly input factors affect the output.
Forms the foundation for many advanced algorithms — Understanding Linear Regression helps in learning more complex ML techniques.

When to Use Linear Regression? Typical Real‑World Examples

Linear Regression is useful when there is a linear relationship between variables — meaning one value changes more or less in proportion to another.

Some common real‑world examples:

Predicting house prices based on area, location, number of bedrooms, etc.
Predicting sales revenue based on marketing spends or advertisement budget.
Predicting student performance based on study hours and attendance.
Predicting crop yield based on rainfall and fertilizers used.
Predicting fuel consumption based on distance or speed.

Simple relatable example:

Suppose you want to estimate the price of a fan. You observe:

A 400‑watt fan costs ₹2000
A 600‑watt fan costs ₹3000

Clearly, when watt increases, price increases. So if someone asks the price of a 500‑watt fan, you can estimate it to be around ₹2500. This estimation using a straight‑line pattern is the core idea of linear regression.

The Linear Relationship & Best Fit Line

Before understanding how Linear Regression trains a model, we need to explore the meaning of a linear relationship and the concept of the best‑fit line.

Independent vs Dependent Variables

In Linear Regression, two types of variables are used:

Independent Variable (Input / Feature / X): The factor that influences or predicts the outcome.
Dependent Variable (Output / Target / Y): The value we want to predict.

For example:
If study hours increase, marks increase. So —

Study hours → Independent variable (X)
Marks → Dependent variable (Y)
Because marks depend on study hours.

Visualizing a Linear Relationship (Scatter Plot + Line)

Real‑world data points are plotted as dots on a graph. For example, plotting study hours vs marks creates a scatter plot.
When these dots roughly form an upward or downward pattern, they represent a linear relationship:

If X increases and Y increases → Positive linear relationship
If X increases and Y decreases → Negative linear relationship

Linear Regression tries to draw a straight line that best represents this pattern. This straight line becomes the best‑fit line.

Equation of the Straight Line:

\displaystyle \bold y = mx + b

Symbol	Meaning
$x$	Independent variable (input feature)
$y$	Predicted output (target variable)
$m$	Slope of the best-fit line
$b$	Intercept — predicted value of $y$ when $x = 0$

Meaning of Slope (m)

The slope tells how much Y changes when X changes.

If m > 0 → As X increases, Y increases
If m < 0 → As X increases, Y decreases
If m = 0 → X has no effect on Y

Meaning of Intercept (b)

The intercept is the value of Y when X is zero. It represents the starting point of the line.

Example: If the equation is
$(y = 8x + 30)$
Then even if a student studies 0 hours, expected marks are 30 → this is the intercept.

What “Best‑Fit Line” Means — Error Minimization

We can draw many lines on a scatter plot, but the best‑fit line is the one that has the least total error.

Error = Actual value – Predicted value

Linear Regression evaluates multiple possible lines and selects the one for which the total error is smallest. In simple words:

The best‑fit line is the one that stays closest to most data points so that predictions become most accurate.

The core idea: Linear Regression finds a straight‑line equation that best captures the relationship between input (X) and output (Y) while minimizing prediction errors.

Aap is poore section ko WordPress + QuickLaTeX ke liye is tarah likh sakte ho.
Neeche ready-to-paste version diya hai jisme text normal hai aur sirf equations me hain — bilkul professional ML tutorial style me.

Hypothesis / Model Function in Linear Regression

Now that we understand the best-fit line concept, the next step is learning how Linear Regression represents this line mathematically.
A machine learning model cannot follow the instruction “draw a straight line”, so it needs a formula that takes input and returns a prediction. This formula is called the Hypothesis Function or Model Function.

In simple terms:

The hypothesis function is the mathematical equation the model uses to predict the value of the target variable (output) from the input variable(s).

Simple Linear Regression — One Feature

When we have only one input feature, the hypothesis function looks like:

$\displaystyle h(x) = \beta_0 + \beta_1 x$

Where:

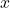$x$ → Input value (Independent variable)
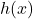$h(x)$ → Predicted value (Dependent variable / target)
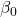$\beta_0$ → Intercept (Prediction when $x = 0$ )
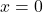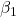$\beta_1$ → Slope (How much the target value changes when 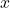$x$ changes)

This formula represents a straight-line relationship between X and Y.

Example

Suppose we want to predict student marks based on study hours.
The model discovers the equation:

$\displaystyle h(x) = 12 + 7x$

If a student studies 0 hours (x = 0), predicted marks = 12
If a student studies 4 hours, predicted marks =
$\displaystyle 12 + 7 \times 4 = 40$

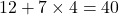
So, the hypothesis function converts input (hours studied) into output (marks).

Multiple Linear Regression — Many Features

If the model uses more than one input variable, the hypothesis function becomes:

$\displaystyle h(x_1, x_2, \ldots, x_k) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_k x_k$

Here:

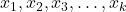$\displaystyle x_1, x_2, x_3, \ldots, x_k$ → Multiple input features
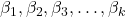$\displaystyle \beta_1, \beta_2, \beta_3, \ldots, \beta_k$ → Coefficients showing how strongly each input affects the target value

Real-life example:

To predict a house price, the model may consider:

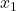$\displaystyle x_1$ = area (sq ft)
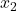$\displaystyle x_2$ = number of bedrooms
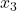$\displaystyle x_3$ = location rating

A possible hypothesis function could be:

Each feature contributes to the final prediction.

Hypothesis in Matrix Form — Optional but Useful

When the number of input features becomes very large, writing the full equation becomes difficult.
So Linear Regression uses a matrix representation for efficient computation:

This does not change the meaning of the model — it only helps the computer perform faster calculations using linear algebra.

Summary Table

h(x_1, x_2, \ldots, x_k) = \beta_0 + \beta_1 x_1 + \ldots + \beta_k x_k

Type of Regression	Hypothesis Formula
Simple Linear Regression
Multiple Linear Regression
Matrix Representation (Optional)

In the simplest words:

The hypothesis function is the mathematical formula that Linear Regression uses to convert input values into predictions.

Assumptions of Linear Regression

For Linear Regression to work correctly and give reliable predictions, certain underlying conditions called assumptions must be satisfied. These assumptions ensure that the mathematical foundation of the model remains valid and the predictions remain meaningful. If these assumptions are violated, the model may still run, but its results (coefficients, predictions, and statistical significance) may become inaccurate.

Below are the key assumptions explained in simple language with relatable examples:

Linearity (Relationship is Linear)

Linear Regression assumes that the relationship between input (X) and output (Y) is linear — meaning that as X increases or decreases, Y also increases or decreases in a consistent and proportional manner.

Example:

Study hours ↑ → Marks ↑ (mostly in a straight‑line pattern)
House area ↑ → House price ↑

If the relationship is curved (e.g., Y increases up to a point and then decreases), Linear Regression is not suitable without modifications.

Independence of Errors

The errors (differences between actual and predicted values) should be independent of each other. In simple terms, the prediction mistake for one observation must not influence the prediction mistake for another.

Example:
If predicting sales for Day 1 has nothing to do with the error on Day 2, independence exists. But if Day 2 sales always depend on Day 1 sales (like festival seasons), this assumption might break.

Homoscedasticity (Constant Variance of Errors)

Linear Regression assumes the error spread remains consistent for all levels of the independent variable.

Meaning: The prediction errors should not become wider or narrower as X changes.

Example:
If predicting student marks:

For low study hours → prediction error is small
For high study hours → prediction error becomes very large

This inconsistency is called heteroscedasticity, which violates the assumption.

Normality of Error Terms

The error values should follow a normal (bell‑shaped) distribution. This does not mean the input or output must be normally distributed — only the errors need to be.

Why this matters:

Helps the model make accurate confidence intervals and hypothesis testing

If the error terms are extremely skewed or have many outliers, this assumption fails.

No Multicollinearity (in Multiple Regression)

In multiple linear regression, the input features should not be highly correlated with each other.

Example of multicollinearity:

Using both “size of house” and “total built‑up area” as features (they mean almost the same thing)

When two features give almost the same information, the model gets confused about which one is more important, leading to unstable coefficient values.

No Autocorrelation (especially for Time‑Series Data)

Autocorrelation means when errors are related to each other over time.
This is especially common in time‑series data (stock prices, daily temperature, etc.).

Example:

If the model underpredicts sales today and also underpredicts tomorrow, the errors are correlated — violating this assumption.

When autocorrelation is present, the model’s predictions become systematically biased.

Additivity of Effects

Linear Regression assumes that each input variable contributes to the output independently and additively.

Meaning:

Final prediction = contribution of feature 1 + contribution of feature 2 + …

It does not consider interactions automatically unless we explicitly add them (interaction terms, polynomial terms, etc.).

Example:

Effect of studying 8 hours + good sleep might be higher together than individually — this interaction is not captured naturally in basic Linear Regression.

In Simple Words

For Linear Regression to give trustworthy predictions:

Relationship must be linear
Errors should behave properly (independent, normally distributed, constant spread, no time patterns)
Input features should not duplicate information
Each input must add to the output independently

Types of Linear Regression

Linear Regression is not a single technique — it comes in different forms depending on the number of input variables and the shape of the relationship between the inputs and the output. Understanding the types helps us choose the right regression model for a given problem.

Simple Linear Regression (One Predictor)

Simple Linear Regression is used when there is only one independent variable (input/feature) and one dependent variable (output). It analyzes how a single input affects the output using a straight-line relationship.

Formula:
$\displaystyle \boldsymbol{y = \beta_0 + \beta_1 x}$
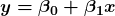
Here: x is the single predictor and y is the predicted value.

Example:

Predicting marks based on study hours.

Input (X) → Study hours
Output (Y) → Marks scored

As study hours increase or decrease, marks typically increase or decrease proportionally. Simple Linear Regression finds the best straight‑line equation that represents this pattern.

Multiple Linear Regression (Multiple Predictors)

Multiple Linear Regression is used when there are two or more input features affecting the output. It captures how multiple variables together contribute to the prediction.

Formula:
$\displaystyle \boldsymbol{y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_k x_k}$
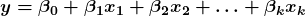
Each predictor has its own coefficient, showing how strongly it influences the target.

Example:

Predicting house price based on:

Area (sq ft)
Number of bedrooms
Location rating

Multiple Linear Regression studies how all these factors combine to determine the final price.

Polynomial Regression (Extended Variant of Linear Regression)

Sometimes the relationship between input and output is not perfectly straight, but still predictable. In such cases, we extend linear regression into Polynomial Regression, where we include powers of the input variable (x², x³, etc.) to capture curves.

Formula:

$\displaystyle \boldsymbol{y = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 + \ldots + \beta_n x^n}$

Even though the graph is curved, the model is still called linear regression because the coefficients (β) remain linear.

Example:

Predicting car mileage based on speed:

Mileage increases when the speed increases up to a point, but after high speeds it decreases.

This forms a curve, not a straight line — polynomial regression can model such patterns better than simple or multiple regression.

Summary Table

Type of Regression	Number of Predictors	Shape of Relationship
Simple Linear Regression	1	Straight line
Multiple Linear Regression	2 or more	Straight line
Polynomial Regression	1 or more	Curved (but linear in coefficients)

In simple words:

Choose Simple when there is one input, Multiple when there are many inputs, and Polynomial when the pattern is curved rather than straight.

Cost / Loss Function & Optimization

Linear Regression learns by trying to make predictions as close as possible to the actual values. To measure how far the predictions are from reality, the model uses a mathematical tool called the Cost (Loss) Function. The goal of the algorithm is to minimize this cost, meaning the model improves until it makes the least possible error.

What is the Cost (Loss) Function for Linear Regression? – Mean Squared Error (MSE)

The Cost Function evaluates how accurate the model’s predictions are. It calculates the difference between actual values and predicted values.

The most commonly used cost function in Linear Regression is Mean Squared Error (MSE):

\displaystyle \boldsymbol{J(\theta) = \frac{1}{n}\sum_{i=1}^{n}\left(y_i – \hat{y}_i\right)^2}

Where:

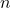$n$ → number of training samples
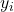$y_i$ → actual value from the dataset
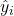$\hat{y}_i$ → value predicted by the model
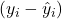$(y_i - \hat{y}_i)$ → prediction error (residual)

The error is squared to ensure it is always positive and to punish large mistakes more heavily. Then the average of all squared errors is taken.

The lower the MSE, the better the model.

Why Minimize Squared Error (Residuals)?

You might ask—why square the error instead of just subtracting?

There are three reasons:

Without squaring, positive and negative errors could cancel each other.
Squaring increases the penalty on large errors, encouraging the model to avoid them.
The smooth curve created by squared errors makes mathematical optimization easier.

So minimizing squared error means:

The model adjusts parameters (slope and intercept / β coefficients) so predictions become as close as possible to the real values.

Introduction to Optimization / Finding Optimal Coefficients

After defining the cost function, the next step is to reduce it. This is where optimization comes in.

Optimization refers to the process of finding the ideal values of the coefficients ( $\beta_0, \beta_1, \ldots$ ) that minimize the cost function.

In Linear Regression, two main methods exist:

Gradient Descent (most widely used) — gradually updates coefficients step‑by‑step to reduce the cost
Normal Equation — direct mathematical solution (works well for small datasets but not large, high‑dimensional ones)

Gradient Descent – Intuitive Analogy

Imagine you are standing on a hill in the dark and your goal is to reach the lowest point of the valley.

You cannot see the ground, but you feel the slope under your feet.
You take a small step downward.
Then again you feel the slope and step downward.
Eventually, you reach the lowest point.

This is exactly how Gradient Descent works:

The hill = the cost function graph
The lowest point = minimum cost (best model)
Each step downward = adjusting coefficients to reduce error

If the step size is too big → you overshoot and miss the lowest point.
If the step size is too small → learning becomes very slow.

Key Takeaways

The cost function tells how wrong the model is.
Linear Regression uses Mean Squared Error (MSE) to measure error.
Training the model means minimizing the cost.
Optimization (especially Gradient Descent) helps find the best-fit coefficients that produce the lowest error.

This naturally leads into the next topic:
Gradient Descent — How the Model Learns Step by Step

Gradient Descent for Linear Regression

Gradient Descent is one of the most important concepts in machine learning because it explains how a model learns. In Linear Regression, Gradient Descent is used to gradually improve the values of the model’s parameters (coefficients) so that the cost/loss becomes minimum.

In simple words:

Gradient Descent repeatedly adjusts the slope and intercept of the line until the error between predicted and actual values becomes as small as possible.

Concept of Gradient Descent (Iteration, Learning Rate, Updates)

Gradient Descent does not find the best parameters in one step. Instead, it follows a step‑by‑step learning process:

Start with random values of parameters (slope and intercept)
Measure error using the cost function (MSE)
Update parameters to reduce error
Repeat the process until error becomes minimum

These repeated steps are called iterations.

The amount of change applied to the parameters each step is controlled by a constant called the learning rate (α).

If the learning rate is too small → learning is slow
If the learning rate is too large → the model may overshoot the optimal point and fail to learn

So Gradient Descent finds the best balance and slowly moves the model toward the best coefficients.

Derivation of Update Rules for Simple Linear Regression

\displaystyle \boldsymbol{y = mx + b}

Gradient Descent updates both m (slope) and b (intercept) during training.

\displaystyle \boldsymbol{m = m – \alpha \frac{\partial J}{\partial m}}

\displaystyle \boldsymbol{b = b – \alpha \frac{\partial J}{\partial b}}

Where:

α = learning rate
∂J/∂m and ∂J/∂b = partial derivatives of the cost function with respect to parameters

These derivatives tell us which direction to move to reduce the cost.

Think of derivatives as directions that point toward the lowest error.

With each iteration, m and b get closer to their optimal values, reducing prediction error.

Convergence Issues: Learning Rate and Local Minima

A successful Gradient Descent must converge, meaning it must reach the lowest possible cost.

Convergence challenges:

Learning rate too high → cost may increase instead of decrease
Learning rate too low → model takes too long to learn

In some machine‑learning models, cost function curves have multiple minima, and Gradient Descent might get stuck in a local minimum.
However, Linear Regression does not have this problem because its cost function is convex (bowl‑shaped).

Therefore, Gradient Descent in Linear Regression always converges to the global minimum — the best possible solution.

Alternative: Normal Equation / Closed‑Form Solution

There is another way to compute the best coefficients without running Gradient Descent — called the Normal Equation.

Instead of iteratively learning, Normal Equation computes optimal coefficients in one shot using linear algebra.

\displaystyle \boldsymbol{\theta = (X^T X)^{-1} X^T y}

Where θ represents all coefficients.

Comparison:

Gradient Descent	Normal Equation
Iterative method	Direct mathematical formula
Works for large datasets	Becomes slow for very high dimensions
Requires learning rate	No learning rate required
Easy for big data	Computationally heavy for big matrices

Summary of Gradient Descent in Linear Regression

Gradient Descent is an optimization algorithm used to reduce prediction error
It updates model parameters using learning rate and cost function derivatives
In Linear Regression, Gradient Descent always finds the best solution because the cost function is convex
Normal Equation is a non‑iterative alternative but less scalable for huge datasets

This completes the foundational understanding of how Linear Regression learns. The next logical step is implementation and evaluation.

Implementing Linear Regression in Python

After understanding the theory of Linear Regression, the next step is to learn how to practically implement it using Python. For this implementation, we will use easy-to-understand examples and the most popular machine learning library: scikit-learn.

We will build a complete regression model step by step — from loading data, training the model, making predictions, to visualizing the results.

Required Libraries

To implement Linear Regression, we need the following Python libraries:

NumPy – for numerical operations
pandas – for loading and handling datasets
scikit-learn – for implementing Linear Regression
matplotlib – for visualization (plotting graph of regression line)

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
Code language: JavaScript (javascript)

Generating / Loading a Dataset

To understand the concept clearly, let’s start with a simple dataset: Study hours vs Marks scored.

# Create a simple dataset
hours = np.array([1, 2, 3, 4, 5, 6]).reshape(-1, 1)
marks = np.array([35, 45, 50, 60, 65, 75])
df = pd.DataFrame({'Hours': hours.flatten(), 'Marks': marks})
print(df)
Code language: PHP (php)

Later, the same method can be applied to any real-world dataset such as house prices, salaries, sales, etc.

Splitting Data (Train/Test)

We divide the data into two parts:

Training set → used to train the model
Test set → used to check how well the model performs on unseen data

X_train, X_test, y_train, y_test = train_test_split(hours, marks, test_size=0.2, random_state=42)

Fitting a Model Using Scikit‑Learn

model = LinearRegression()
model.fit(X_train, y_train)

This step teaches the model the best fit line by calculating the slope and intercept.

Inspecting Model Coefficients (Slope/Intercept)

print("Slope (m):", model.coef_[0])
print("Intercept (b):", model.intercept_)
Code language: CSS (css)

Example output may look like:

Slope (m): 8.5
Intercept (b): 28.4
Code language: CSS (css)

This means our learned equation is:

y = 8.5 × Hours + 28.4

Making Predictions and Visualising Regression Line

# Predict marks for test set
predictions = model.predict(X_test)
print(predictions)

# Plot graph
plt.scatter(hours, marks, color='blue')
plt.plot(hours, model.predict(hours), color='red')
plt.xlabel('Study Hours')
plt.ylabel('Marks Scored')
plt.title('Linear Regression Example')
plt.show()
Code language: PHP (php)

Blue dots → actual data points
Red line → best-fit regression line

This visual graph helps us understand how well the model captures the pattern.

Evaluating the Model

To measure how good our model is, we calculate evaluation metrics (explained in the next section). Example:

from sklearn.metrics import r2_score
print("R² Score:", r2_score(y_test, predictions))
Code language: JavaScript (javascript)

A value close to 1 indicates excellent performance.

Final Code Snippet (Full Program Together)

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt

# Dataset
hours = np.array([1, 2, 3, 4, 5, 6]).reshape(-1, 1)
marks = np.array([35, 45, 50, 60, 65, 75])

# Split data
X_train, X_test, y_train, y_test = train_test_split(hours, marks, test_size=0.2, random_state=42)

# Train model
model = LinearRegression()
model.fit(X_train, y_train)

# Model parameters\...Code language: PHP (php)

Evaluation Metrics for Linear Regression

Once we train a Linear Regression model, we cannot assume it is good just because it produces numerical predictions. We must verify how close the predictions are to the true values. This is where evaluation metrics come in. These metrics mathematically quantify the model’s performance.

Think of it like testing a bow and arrow:

“Actual values” = the center of the target
“Predicted values” = where the arrows land The closer the arrows are to the center, the better the model.

Different metrics tell different things about prediction quality — no single metric is ideal in all scenarios. Below is a complete breakdown of all major Linear Regression performance metrics.

Mean Squared Error (MSE)

MSE measures the average of the squared errors — where error = difference between actual and predicted value.

\displaystyle \boldsymbol{MSE = \frac{1}{n}\sum_{i=1}^{n}\left(y_i – \hat{y}_i\right)^2}

Why square the errors?

To ensure negative and positive errors do not cancel each other out.
To punish large mistakes more strongly.

Example: Actual values = [50, 60, 70]
Predicted values = [48, 62, 65]

Errors = (50 − 48) = 2, (60 − 62) = −2, (70 − 65) = 5
Squared errors = 4, 4, 25

\displaystyle \boldsymbol{MSE = \frac{4 + 4 + 25}{3} = 11}

Low MSE means the model is good. ✘ But because errors are squared, units become squared (e.g., price becomes price²).

Mean Absolute Error (MAE)

MAE measures the average of the absolute errors (without squaring).

\displaystyle \boldsymbol{MAE = \frac{1}{n}\sum_{i=1}^{n}\left|y_i – \hat{y}_i\right|}

📌 Example using earlier values: Absolute errors = 2, 2, 5

\displaystyle \boldsymbol{MAE = \frac{2 + 2 + 5}{3} = 3}

✔ MAE is very easy to understand. ✔ Less sensitive to extreme outliers. ✘ Does not punish large mistakes as strongly as MSE.

Real‑life analogy: MAE = “On average, our arrow misses the target center by 3 units.”

Root Mean Squared Error (RMSE)

RMSE is simply the square‑root of MSE.

\displaystyle \boldsymbol{RMSE = \sqrt{MSE}}

From our example:

\displaystyle \boldsymbol{RMSE = \sqrt{11} \approx 3.31}

✔ RMSE is easier to interpret because it is in the same unit as the target variable. ✔ Best when large errors must be penalized. ✘ Sensitive to extreme values.

Real‑life analogy: RMSE = “Our predictions are off by about 3.31 marks on average.”

Coefficient of Determination — R² Score

R² measures how well the model explains the variance of the target variable.

\displaystyle \boldsymbol{R^2 = 1 – \frac{SS_{res}}{SS_{tot}}}

Where:

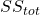$SS_{tot}$ → total variation in actual values
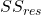$SS_{res}$ → remaining variation after model predictions
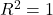$R^2 = 1$ → Perfect prediction
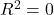$R^2 = 0$ → Model is no better than predicting the mean

\displaystyle R^2 < 0

→ Model is worse than a constant prediction

Example:
$R^2 = 0.92$ means 92% of the variation in the target is explained by the model.

Adjusted R² — Important for Multiple Regression

When more features are added to a model, $R^2$ always increases — even if the new feature adds no predictive value.

Adjusted R² fixes this by penalizing unnecessary features.

If a new feature improves prediction → Adjusted 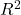$R^2$ increases
If a new feature is useless → Adjusted 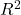$R^2$ drops

Best for evaluating multiple regression models. Not useful for single‑feature regression.

Which Metric Should You Use? (Pros & Cons)

Metric	Best When	Strengths	Weaknesses
MAE	You want general average error	Simple, intuitive	Large errors not penalized strongly
MSE	Large mistakes are costly	Strong penalty on large errors	Squared units are hard to interpret
RMSE	Scale of error must be in real units	Easy to explain to non‑technical users	Sensitive to outliers
R²	Explaining model fit	Single score explanation	Misleading with many features
Adjusted R²	Comparing multi‑feature models	Penalizes irrelevant features	Only valid when R² is present

Intuitive Summary (Remember This)

Situation	Best Metric
Want simple accuracy	MAE
Want to punish big mistakes	MSE or RMSE
Want to compare model fits	R²
Want to compare multi‑feature models	Adjusted R²

Practical Example in Python

from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np

actual = np.array([50, 60, 70])
pred = np.array([48, 62, 65])

mse = mean_squared_error(actual, pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(actual, pred)
r2 = r2_score(actual, pred)

print("MSE:", mse)
print("RMSE:", rmse)
print("MAE:", mae)
print("R2 Score:", r2)Code language: PHP (php)

Advantages and Limitations of Linear Regression

Linear Regression is one of the simplest and most widely used machine learning algorithms. Although it is highly popular, it is important to understand both its strengths and weaknesses. This helps us decide when it is appropriate to use Linear Regression and when it is not.

Advantages of Linear Regression

Linear Regression has remained popular for decades because of its practical and theoretical benefits.

Simplicity and Ease of Implementation

The mathematical idea behind Linear Regression is easy to understand. It models a relationship using a straight line, making it one of the most beginner‑friendly algorithms.

Requires less computational power
Does not need high‑end hardware
Quick to test and experiment

Interpretability – Easy to Understand How Predictions Are Made

Unlike black‑box models (e.g., Neural Networks), Linear Regression clearly shows how each feature affects the prediction through its coefficients.

Positive coefficient → increases result
Negative coefficient → decreases result
Magnitude shows strength of impact

This makes Linear Regression very valuable in fields like finance, medical research, economics where understanding the impact of variables is crucial.

Good Baseline Model

Even when Linear Regression is not the final solution, it works as a good baseline to compare more complex algorithms.

Helps determine whether more advanced models are necessary
If Linear Regression performs poorly, non‑linear models may be needed

Efficient for Large Datasets with Many Samples

Linear Regression performs well when there are many examples (rows) in the dataset, and training is computationally efficient compared to many other algorithms.

Limitations of Linear Regression

Although powerful, Linear Regression is not suitable for every kind of problem.

Assumes Linearity in Data

Linear Regression works only when the relationship between input and output is roughly linear.

If the data has curves or patterns → Linear Regression may fail
May oversimplify relationships and give inaccurate predictions

Example: Predicting salary based on experience is roughly linear, but predicting customer purchase probability from browsing behaviour is not.

Highly Sensitive to Outliers

A few unusually high or low values can drastically influence the model.

Outliers distort slope and intercept
Leads to large prediction error

Example: A house that is 20× bigger than average may mislead the model.

Multicollinearity Problem in Multiple Regression

When independent variables are strongly correlated with each other, the model becomes unstable.

Coefficients fluctuate widely
Interpretation becomes unreliable

Solution:

Remove highly correlated features
Use PCA or regularization techniques

Feature Engineering Required

Linear Regression does not automatically learn complex patterns.

Polynomial features, interactions, transformations are often needed
Requires manual effort and domain knowledge

May Underfit Complex Real‑World Data

Many real‑world phenomena are not linear.
If the model is too simple for the problem, it will underfit, meaning:

Very low training accuracy
Very low testing accuracy
Model is too basic to capture real patterns

Example: Stock market prediction cannot be solved reliably using just Linear Regression.

Summary Table: When to Use and When to Avoid Linear Regression

Situation	Recommended?	Reason
Relationship is linear	✅ Yes	Linear Regression will perform well
Dataset contains many outliers	❌ Avoid	Predictions will be distorted
Independent variables are highly correlated	❌ Avoid	Model becomes unstable
Need simple and interpretable model	✅ Yes	Coefficients explain effects clearly
Real‑world phenomenon is complex / non‑linear	❌ Avoid	Model may underfit
Need quick baseline / benchmark model	✅ Yes	Fast, lightweight, reliable